EDA zbioru danych Irysy

Wiedza domenowa

Przedmiotem EDA będzie zbiór danych związany z kwiatami irysy. Irysy to piękne, wieloletnie rośliny ozdobne należące do rodziny kosaćcowatych (Iridaceae). Znane są ze swoich charakterystycznych, eleganckich kwiatów, które występują w szerokiej gamie kolorów, od bieli i żółci po fiolet i niebieski. Każdy kwiat irysa składa się z trzech wzniesionych płatków wewnętrznych oraz trzech skierowanych w dół działek kielicha, które często przyjmują formę "brody" na środku.

Irysy są popularne w ogrodach na całym świecie ze względu na swoją urodę, a także różnorodność form i kolorów. Szczególnie cenionymi gatunkami są Iris setosa, Iris versicolor i Iris virginica, które są również częścią klasycznego zbioru danych używanego w analizie statystycznej i uczeniu maszynowym. Te kwiaty nie tylko dodają estetyki do krajobrazów, ale także stanowią doskonały temat badań ze względu na wyraźne różnice między gatunkami, co czyni je idealnym modelem do nauki o klasyfikacji danych.

Rodzaje Irysów

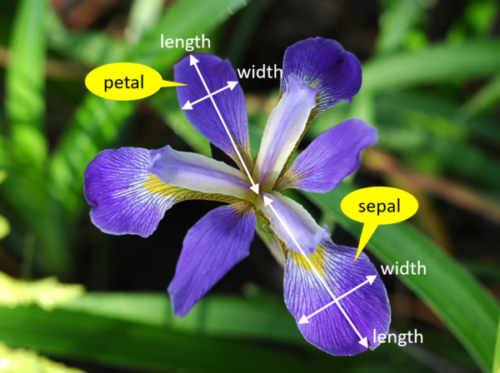
Podstawowe wymiary

Wstępna analiza danych

Na samym początku zostanie przeprowadzona krótka analiza ogólnego zarysu zbioru danych, m.in. sprawdzając losowe rekordy lub wartości unikatowe.

Losowe 5 rzędów

• istnieją cztery główne wymiary (dł. i szer. kielicha oraz dł. i szer. płatka),
• wyróżniamy trzy rodzaje irysów,
• każdy irys ma odmienne wymiary (zależnie od rodzaju).

długość kielicha (sepal length)	szerokość kielicha (sepal width)	długość płatka (petal length)	szerokość płatka (petal width)	klasa (class)
6.3	2.5	4.9	1.5	Iris-versicolor
6.8	3.0	5.5	2.1	Iris-virginica
6.4	2.8	5.6	2.2	Iris-virginica
5.6	3.0	4.1	1.3	Iris-versicolor
4.9	3.1	1.5	0.1	Iris-setosa

Wartości unikatowe

Kolumna	Liczba unikatowych wartości
długość kielicha (sepal length)	35
szerokość kielicha (sepal width)	23
długość płatka (petal length)	43
szerokość płatka (petal width)	22
klasa (class)	3

Statystyki opisowe

	count	mean	std	min	25%	50%	75%	max
długość kielicha (sepal length)	150.0	5.84	0.83	4.3	5.1	5.80	6.4	7.9
szerokość kielicha (sepal width)	150.0	3.05	0.43	2.0	2.8	3.00	3.3	4.4
długość płatka (petal length)	150.0	3.76	1.76	1.0	1.6	4.35	5.1	6.9
szerokość płatka (petal width)	150.0	1.20	0.76	0.1	0.3	1.30	1.8	2.5

Podsumowanie wstępnej analizy:

• zbiór danych zawiera 150 pomiarów irysów dla trzech rodzajów,
• najmniejszy rozrzut od średniej występuje dla szerokości kielicha, gdzie średnia ~ mediana,
• największy rozrzut pomiarów wystąpił dla długości płatka,
• minimalny pomiar wyniósł 0.1 cm dla szerokości płatka - warto by było ustalić jakie narzędzie pomiarowe zostało zastosowane do tak małej wartości pomiaru,
• z wartości unikatowych wynika, że największa powtarzalność jest przy długości płatka (ok. 29%), natomiast najmniejsza przy szerokości płatka i szerokości kielicha (ok. 15%),
• wszystkie różnice w pomiarach mogą wynikać z błędu pomiarowego.

Analiza wartości brakujących

Sprawdzenie czy w danym zbiorze danych znajdują się wartości brakujące, które mogłyby zaburzyć końcowe wyniki.

Ilościowe zestawienie brakujących wartości w analizowanym zbiorze danych:

Kolumna	Liczba brakujących wartości
długość kielicha (sepal length)	0
szerokość kielicha (sepal width)	0
długość płatka (petal length)	0
szerokość płatka (petal width)	0
klasa (class)	0

Podsumowanie analizy wartości brakujących:

• nie ma żadnych brakujących wartości,
• dane są precyzyjne i nie trzeba ich modyfikować.

Analiza pojedynczych wartości

Żeby jak najlepiej zrozumieć wszelkie korelacje pomiędzy danymi oraz ich istotność - należy najpierw zgłębić wiedzę dotyczącą pojedynczych rekordów.

Histogramy

Histogram irys-setosa:

Histogram wymiarów Irys-virginica:

Histogram dla irys-versicolor:

Wnioski płynące z histogramów:

• irys-setos mają najczęstsze szer. płatka ~0.2 cm (prawie 30 pomiarów w tym zakresie),
• dla trzech rodzajów irysa: szer. kielicha najczęściej mieści się od 2.75 do 3.5 cm,
• pod względem wielkości tak prezentują się rodzaje irysów w kolejności rosnącej: irys-setosa -> irys-versicolor -> irys-virginica.

Wykres liniowy przedstawiający zakres pomiarów:

• można zauważyć, że dł. płatka ma największe rozrzuty pomiędzy rodzajami irysa (najmniejsze wartości dla irys-setos),
• szer. kielicha to wymiar, który ma najbardziej zbliżone wartości dla wszystkich rodzajów irysa.

Wykresy słupkowe

Barplot dla szerokości płatka:

• najczęstszym pomiarem był pomiar szer. płatka dla irysa-setosa (pomiar ~0.2 cm stanowił ~19% wszystkich pomiarów),
• zachowana jest zależność, że szer. płatka wzrasta ze zmianą rodzaju irysa.

Barplot dla długości płatka:

• zachowana jest zależność, że szer. płatka wzrasta ze zmianą rodzaju irysa.

Barplot dla szerokości kielicha:

• w odróżnieniu do wymiarów płatka -> irys-setos posiada najszerszy kielich,
• najbardziej rozrzucone pomiary są dla iris-versicolor (od 2.5 aż do 3.4 cm),
• najczęściej występuje szerokość kielicha ~3cm (szczególnie w przypadku irysa-virginica).

Barplot dla długości kielicha:

• najbardziej rozrzucone pomiary są dla iris-versicolor (od 4.9 aż do 6.7 cm),
• najmniejszą dł. kielicha ma iris-setosa a największą iris-virginica,
• dla irysa-virginica kilka pomiarów było zauważalnie mniejszych od pozostałych.

Podsumowanie analizy pojedynczych wartości:

• najczęstszy pomiar szerokości płatka występuje dla irysa-setosa i wynosi ~0.2 cm (co stanowi niemal 20% pomiarów),
• wymiary płatka (szer. oraz dł.) rosną wraz ze zmianą rodzaju irysa: setosa->versicolor->virginica,
• najmniejsze płatki mają irysy-setosa,
• dla trzech rodzajów irysa: szer. kielicha najczęściej mieści się od 2.5 do 3.5 cm, co pokazuje, że na ten wymiar ma najmniejszy wpływ rodzaj irysa,
• w odróżnieniu do wymiarów płatka -> irys-setos ma najszerszy kielich ze wszystkich irysów,
• najwiekszy rozrzut w pomiarach wymiarów kielicha występuje dla irysa-versicolor,
• najczęściej występuje szer. kielicha ~3 cm (co stanowi 18% wszystkich pomiarów),
• dł. kielicha jest najmniejsza dla irysa-setosa a największa dla irysa-virginica.

Analiza korelacji

Po wstępnym oszacowaniu zarysu danych, zgłębieniu pojedynczych rekordów oraz zweryfikowaniu wartości brakujących - istnieje możliwość zrozumieć korelacyjność danych.

Macierz korelacji dla wymiarów irysa:

• wymiary płatka (szer. i dł.) zależą wzajemnie od siebie,
• na wymiary płatka (szer. i dł.) ma bardzo duży wpływ długość kielicha,
• wymiary kielicha (szer. i dł.) są od siebie niemalże niezależne,
• połowiczna odwrotna korelacja występuje pomiędzy szerokością kielicha a wymiarami płatka.

	szerokość płatka (petal width)	długość płatka (petal length)	szerokość kielicha (sepal width)	długość kielicha (sepal length)
szerokość płatka (petal width)	1.000000	0.962757	-0.356544	0.817954
długość płatka (petal length)	0.962757	1.000000	-0.420516	0.871754
szerokość kielicha (sepal width)	-0.356544	-0.420516	1.000000	-0.109369
długość kielicha (sepal length)	0.817954	0.871754	-0.109369	1.000000

Wykresy punktowe dla rodzajów irysa oraz wymiarów irysa:

• każdy rodzaj irysa ma inne wymiary płatków oraz kielichów.

Wykresy punktowe dla największych korelacji pomiędzy wymiarami irysa:

• Można zaobserwować korelacje dodatnią -> im większa szer. płatka tym większa dł. płatka.

• Można zaobserwować korelacje dodatnią pomiędzy wymiarami płatka a długością kielicha -> im większa dł. kielicha tym większe będą szer. i dł. płatka.

• Większa zależność występuje dla wymiarów: dł. płatka oraz dł. kielicha.

• Pomiędzy dł. a szer. kielicha występuje korelacja zerowa -> te wymiary nie mają na siebie wpływu.

Podsumowanie analizy korelacji:

• wymiary płatka (długość i szerokość) są w korelacji dodatniej,
• wymiary kielicha nie zależą od siebie (korelacja zerowa),
• im większa długość kielicha tym większe wymiary płatka (szer. i dł.),
• rodzaj irysa wpływa ma wymiary kielicha oraz płatka.

Analiza wartości odstających

Aby wysnuć ostateczne wnioski - warto zweryfikować również czy w analizowanym zbiorze danych występują jakieś wartości odstające, które mogłyby wprowadzić niepotrzebny szum do analizy.

Boxplots dla wymiarów irysa w zależności od jego rodzaju

Boxplot dla szerokości płatka:

• wartości odstające wystąpiły tylko dla rodzaju: iris-setosa (2 outliers),
• w przypadku iris-setosa: mediana wyniosła ~0,2 cm (czyli najczęściej występujący pomiar) i była na równi z kwartylem 1 -> co oznacza, że 75% pomiarów było powyżej mediany,
• największy rozrzut w pomiarach widać dla rodzaju: iris-virginica.

Boxplot dla długości płatka:

• wartości odstające wystąpiły dla rodzajów: iris-setosa (3 outliers) oraz iris-versicolor (1 outlier),
• największy rozrzut w pomiarach widać dla rodzaju: iris-virginica.

Boxplot dla szerokości kielicha:

• wartości odstające wystąpiły tylko dla rodzaju: iris-virginica (2 outliers),
• największy rozrzut w pomiarach widać dla rodzaju: iris-setosa.

Boxplot dla długości kielicha:

• wartości odstające wystąpiły tylko dla rodzaju: iris-virginica (1 outlier),
• największy rozrzut w pomiarach widać dla rodzaju: iris-virginica.

Podsumowanie analizy outliers:

• dla wymiarów płatków (szer. i dł.) wartości odstające wystąpiły głównie dla rodzaju: iris-setosa (5) oraz jeden outlier dla iris-versicolor,
• dla wymiarów płatków (szer. i dł.) największy rozrzut w pomiarach wystąpił dla rodzaju: iris-virginica,
• dla wymiarów kielicha (szer. i dł.) wartości odstające wystąpiły jedynie dla rodzaju: iris-virginica (3),
• dla dł. kielicha największy rozrzut w pomiarach wystąpił dla rodzaju: iris-virginica,
• dla szer. kielicha największy rozrzut w pomiarach wystąpił dla rodzaju: iris-setosa,
• w przypadku iris-setosa: mediana była na równi z kwartylem 1 -> co oznacza, że 75% pomiarów było powyżej mediany,
• najmniejszy wpływ rodzaju irysa na wymiary można zauważyć przy szerokości kielicha.

Wnioski końcowe:

Przeanalizowano dane dotyczące irysów, w których znajdowały się trzy rodzaje kwiatów: irys-setosa, irys-versicolor oraz irys-virginica, jak również pomiary związane z kielichem (długość i szerokość) oraz płatkiem (długość i szerokość) poszczególnego irysa. Na podstawie danych - dokonano analizy EDA i wysnuto następujące wnioski:

• rodzaj irysa wpływa na jego wymiary,
• według danych występuje następująca kolejność rosnąca pod względem wielkości kwiatów: iris-setosa -> iris-versicolor -> iris-virginica (z wyłączeniem szer. kielicha - iris-setos cechuje się najszerszym kielichem),
• najczętszym pomiarem był pomiar szerokości płatka dla rodzaju: iris-setosa i wyniósł ~0,2 cm (co stanowiło niemal 20% wszystkich pomiarów).
• szerokość kielicha to wymiar, który ma najbardziej zbliżone wartości dla wszystkich rodzajów irysa,
• długość płatka ma największy rozrzut w pomiarach pomiędzy rodzajami irysa,
• najczęściej spotykana szerokość kielicha wynosi ok. 3 cm.
• wymiary płatka zależą wzajemnie od siebie,
• wymiary kielicha nie zależą od siebie,
• im większa długość kielicha - tym większe wymiary płatka,
• dla wymiarów płatków wystąpiło 5 wartości odstających dla rodzaju: irys-setosa -> może to być spowodowane jego najmniejszymi gabarytami i problematyką samego pomiaru,
• kwiat irys-virginica miał największy rozrzut w pomiarach.