import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error, r2_score
import matplotlib.pyplot as plt
# Tworzenie przykładowych danych mieszkań
np.random.seed(42)
n_mieszkan = 1000
data = pd.DataFrame({
'powierzchnia': np.random.normal(70, 25, n_mieszkan),
'liczba_pokoi': np.random.randint(1, 5, n_mieszkan),
'wiek_budynku': np.random.randint(0, 50, n_mieszkan),
'odleglosc_centrum': np.random.exponential(5, n_mieszkan)
})
# Realistyczna formuła ceny (z szumem)
data['cena'] = (
data['powierzchnia'] * 8000 + # 8k za m²
data['liczba_pokoi'] * 15000 + # 15k za pokój
(50 - data['wiek_budynku']) * 2000 + # starsze = tańsze
data['odleglosc_centrum'] * (-3000) + # dalej = tańsze
np.random.normal(0, 50000, n_mieszkan) # szum losowy
)
print("Podstawowe statystyki:")
print(data.describe())Linear Regression — przewiduj wartości liczbowe
📈 Czym jest Linear Regression?
Linear Regression to jeden z najprostszych i najczęściej używanych algorytmów ML do przewidywania wartości liczbowych (np. ceny, temperatury, sprzedaży). Szuka najlepszej linii prostej, która opisuje zależność między zmiennymi.
💡 Intuicja matematyczna
Szukamy takiej linii y = ax + b, która najlepiej “przechodzi” przez nasze punkty danych. Algorytm automatycznie dobiera optymalne wartości a (slope) i b (intercept).
🏠 Praktyczny przykład: predykcja cen mieszkań
Pokaż statystyki
Podstawowe statystyki:
powierzchnia liczba_pokoi wiek_budynku odleglosc_centrum \
count 1000.000000 1000.000000 1000.000000 1000.000000
mean 70.483301 2.473000 25.049000 4.971457
std 24.480398 1.128958 14.384001 4.883716
min -11.031684 1.000000 0.000000 0.000058
25% 53.810242 1.000000 13.000000 1.459988
50% 70.632515 2.000000 25.000000 3.505541
75% 86.198597 4.000000 38.000000 6.954361
max 166.318287 4.000000 49.000000 34.028756
cena
count 1.000000e+03
mean 6.363187e+05
std 2.004394e+05
min 1.686504e+04
25% 5.049745e+05
50% 6.356690e+05
75% 7.647808e+05
max 1.440259e+06 🔧 Trenowanie modelu krok po kroku
1) Przygotowanie danych
# Sprawdzenie korelacji - które zmienne są najważniejsze?
correlation = data.corr()['cena'].sort_values(ascending=False)
# Podział na features (X) i target (y)
X = data[['powierzchnia', 'liczba_pokoi', 'wiek_budynku', 'odleglosc_centrum']]
y = data['cena']
# Podział train/test (80/20)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
print("Korelacja z ceną:")
print(correlation)
print(f"Dane treningowe: {X_train.shape[0]} mieszkań")
print(f"Dane testowe: {X_test.shape[0]} mieszkań")
Pokaż korelacje oraz dane treningowe
Korelacja z ceną:
cena 1.000000
powierzchnia 0.949080
liczba_pokoi 0.025094
odleglosc_centrum -0.042040
wiek_budynku -0.115566
Name: cena, dtype: float64
Dane treningowe: 800 mieszkań
Dane testowe: 200 mieszkań2) Trenowanie modelu
# Utworzenie i trenowanie modelu
model = LinearRegression()
model.fit(X_train, y_train)
# Sprawdzenie współczynników
print("Współczynniki modelu:")
for feature, coef in zip(X.columns, model.coef_):
print(f"{feature}: {coef:.0f} zł")
print(f"Intercept (stała): {model.intercept_:.0f} zł")
Pokaż współczynniki
Współczynniki modelu:
powierzchnia: 7924 zł
liczba_pokoi: 15811 zł
wiek_budynku: -2108 zł
odleglosc_centrum: -2698 zł
Intercept (stała): 104042 zł3) Ewaluacja wyników
# Predykcje na zbiorze testowym
y_pred = model.predict(X_test)
# Metryki
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"\nWyniki modelu:")
print(f"Mean Absolute Error: {mae:.0f} zł")
print(f"R² Score: {r2:.3f}")
print(f"Średni błąd to {mae/data['cena'].mean()*100:.1f}% ceny mieszkania")
# Przykładowe predykcje
for i in range(5):
rzeczywista = y_test.iloc[i]
przewidywana = y_pred[i]
błąd = abs(rzeczywista - przewidywana)
print(f"Mieszkanie {i+1}: rzeczywista={rzeczywista:.0f}zł, "
f"przewidywana={przewidywana:.0f}zł, błąd={błąd:.0f}zł")
Pokaż wyniki modelu
Wyniki modelu:
Mean Absolute Error: 38912 zł
R² Score: 0.934
Średni błąd to 6.1% ceny mieszkania
Mieszkanie 1: rzeczywista=702313zł, przewidywana=771489zł, błąd=69177zł
Mieszkanie 2: rzeczywista=791174zł, przewidywana=816756zł, błąd=25582zł
Mieszkanie 3: rzeczywista=326702zł, przewidywana=274297zł, błąd=52405zł
Mieszkanie 4: rzeczywista=441380zł, przewidywana=456054zł, błąd=14674zł
Mieszkanie 5: rzeczywista=445427zł, przewidywana=383199zł, błąd=62228zł📊 Wizualizacja wyników
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error, r2_score
import matplotlib.pyplot as plt
# Przykładowe dane mieszkań (powtarzamy dla demonstracji)
np.random.seed(42)
n_mieszkan = 1000
data = pd.DataFrame({
'powierzchnia': np.random.normal(70, 25, n_mieszkan),
'liczba_pokoi': np.random.randint(1, 5, n_mieszkan),
'wiek_budynku': np.random.randint(0, 50, n_mieszkan),
'odleglosc_centrum': np.random.exponential(5, n_mieszkan)
})
data['cena'] = (
data['powierzchnia'] * 8000 +
data['liczba_pokoi'] * 15000 +
(50 - data['wiek_budynku']) * 2000 +
data['odleglosc_centrum'] * (-3000) +
np.random.normal(0, 50000, n_mieszkan)
)
# Przygotowanie i trenowanie modelu
X = data[['powierzchnia', 'liczba_pokoi', 'wiek_budynku', 'odleglosc_centrum']]
y = data['cena']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# Oblicz metryki
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
# Przygotuj wykresy
plt.figure(figsize=(10, 6))
plt.subplot(1, 2, 1)
plt.scatter(y_test, y_pred, alpha=0.6)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=2)
plt.xlabel('Rzeczywiste ceny')
plt.ylabel('Przewidywane ceny')
plt.title('Rzeczywiste vs Przewidywane')
plt.subplot(1, 2, 2)
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.6)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Przewidywane ceny')
plt.ylabel('Residuals (błędy)')
plt.title('Analiza residuals')
plt.tight_layout()
# Zapisz wykres do zmiennej
import io
import base64
buf = io.BytesIO()
plt.savefig(buf, format='png', dpi=100, bbox_inches='tight')
buf.seek(0)
plt.close()
# Przygotuj przykładowe predykcje
przykladowe_predykcje = []
for i in range(3):
rzeczywista = y_test.iloc[i]
przewidywana = y_pred[i]
blad = abs(rzeczywista - przewidywana)
przykladowe_predykcje.append(f"Mieszkanie {i+1}: rzeczywista={rzeczywista:.0f}zł, przewidywana={przewidywana:.0f}zł, błąd={blad:.0f}zł")
print(f"Wyniki modelu Linear Regression:")
print(f"Mean Absolute Error: {mae:.0f} zł")
print(f"R² Score: {r2:.3f}")
print(f"Średni błąd to {mae/data['cena'].mean()*100:.1f}% ceny mieszkania")
print(f"\nPrzykładowe predykcje:")
for pred in przykladowe_predykcje:
print(pred)
# Odtwórz wykres
plt.figure(figsize=(10, 6))
plt.subplot(1, 2, 1)
plt.scatter(y_test, y_pred, alpha=0.6)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=2)
plt.xlabel('Rzeczywiste ceny')
plt.ylabel('Przewidywane ceny')
plt.title('Rzeczywiste vs Przewidywane')
plt.subplot(1, 2, 2)
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.6)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Przewidywane ceny')
plt.ylabel('Residuals (błędy)')
plt.title('Analiza residuals')
plt.tight_layout()
plt.show()
Pokaż wyniki i wykresy analizy
Wyniki modelu Linear Regression:
Mean Absolute Error: 38912 zł
R² Score: 0.934
Średni błąd to 6.1% ceny mieszkania
Przykładowe predykcje:
Mieszkanie 1: rzeczywista=702313zł, przewidywana=771489zł, błąd=69177zł
Mieszkanie 2: rzeczywista=791174zł, przewidywana=816756zł, błąd=25582zł
Mieszkanie 3: rzeczywista=326702zł, przewidywana=274297zł, błąd=52405zł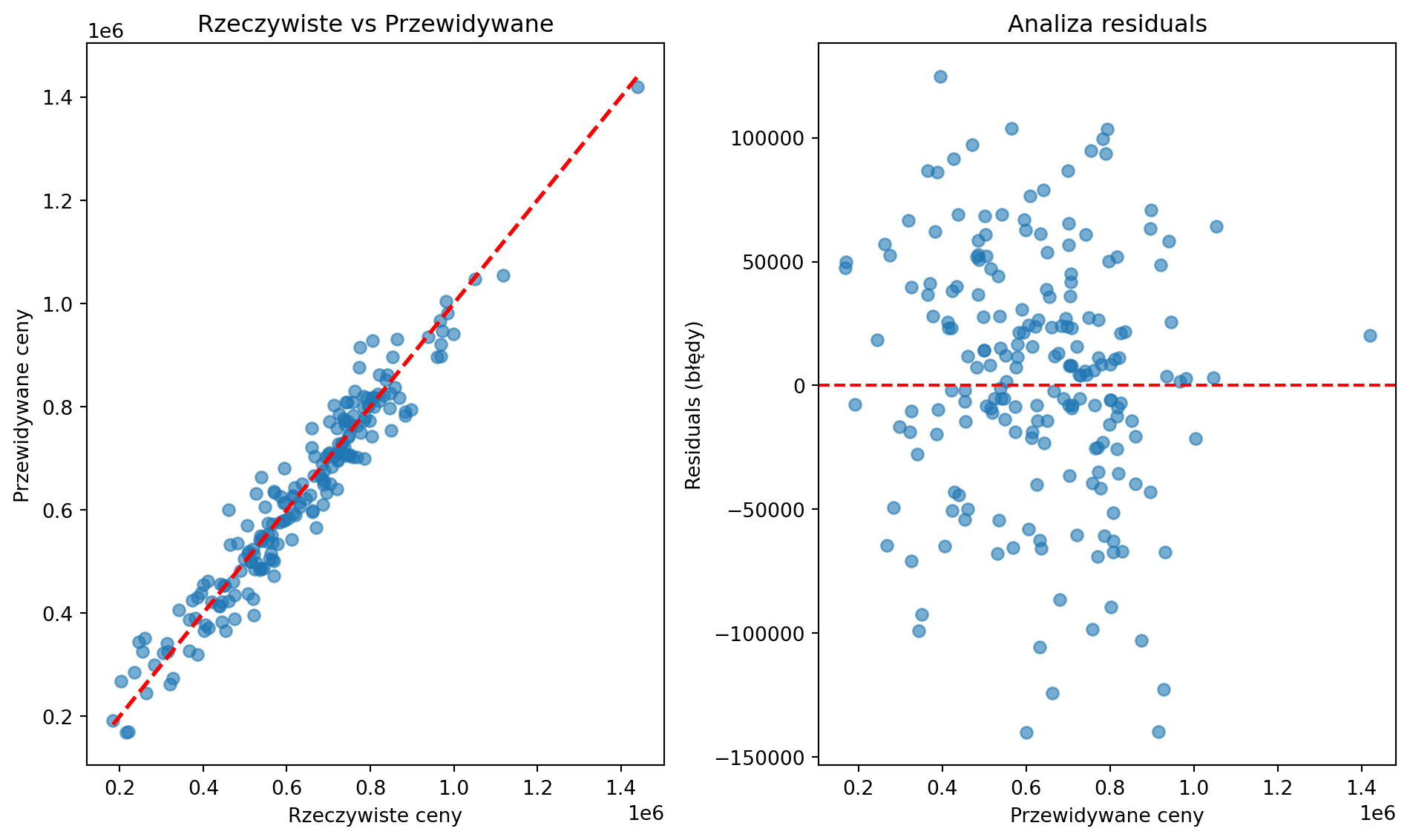
🎯 Praktyczne zastosowania Linear Regression
1) Biznesowe
# Przewidywanie sprzedaży na podstawie budżetu marketingowego
sales_data = pd.DataFrame({
'marketing_budget': [10000, 15000, 20000, 25000, 30000],
'sales': [100000, 140000, 180000, 220000, 260000]
})
model_sales = LinearRegression()
model_sales.fit(sales_data[['marketing_budget']], sales_data['sales'])
# "Jeśli zwiększę budżet do 35k, sprzedaż wzrośnie do:"
new_sales = model_sales.predict([[35000]])
print(f"Przewidywana sprzedaż przy budżecie 35k: {new_sales[0]:.0f}")
Pokaż przewidywaną sprzedaż
Przewidywana sprzedaż przy budżecie 35k: 3000002) Analizy finansowe
# Relacja między PKB a konsumpcją
economics_data = pd.DataFrame({
'pkb_per_capita': [25000, 30000, 35000, 40000, 45000],
'konsumpcja': [18000, 21000, 24000, 27000, 30000]
})
model_econ = LinearRegression()
model_econ.fit(economics_data[['pkb_per_capita']], economics_data['konsumpcja'])
# Współczynnik skłonności do konsumpcji
print(f"Na każde dodatkowe 1000zł PKB, konsumpcja rośnie o: {model_econ.coef_[0]:.0f}zł")
Pokaż współczynnik skłonności do konsumpcji
Na każde dodatkowe 1000zł PKB, konsumpcja rośnie o: 1zł⚠️ Najczęstsze pułapki i jak ich unikać
1) Overfitting z wieloma zmiennymi
# ZŁO: za dużo features względem danych
# Jeśli masz 100 mieszkań, nie używaj 50 features!
# DOBRZE: zasada kciuka
def check_features_ratio(X, y):
ratio = len(y) / X.shape[1]
if ratio < 10:
print(f"⚠️ Uwaga: masz tylko {ratio:.1f} obserwacji na feature!")
print("Rozważ: więcej danych lub mniej features")
else:
print(f"✅ OK: {ratio:.1f} obserwacji na feature")
check_features_ratio(X_train, y_train)
Pokaż wyniki
✅ OK: 200.0 obserwacji na feature2) Sprawdzanie założeń linearności
# Sprawdź czy zależności są rzeczywiście liniowe
from scipy import stats
for col in X.columns:
correlation, p_value = stats.pearsonr(data[col], data['cena'])
print(f"{col}: korelacja={correlation:.3f}, p-value={p_value:.3f}")
if abs(correlation) < 0.1:
print(f"⚠️ {col} ma słabą korelację - może nie być przydatna")
Pokaż wyniki korelacji
powierzchnia: korelacja=0.949, p-value=0.000
liczba_pokoi: korelacja=0.025, p-value=0.428
⚠️ liczba_pokoi ma słabą korelację - może nie być przydatna
wiek_budynku: korelacja=-0.116, p-value=0.000
odleglosc_centrum: korelacja=-0.042, p-value=0.184
⚠️ odleglosc_centrum ma słabą korelację - może nie być przydatna3) Wielokoliniowość (features korelują między sobą)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Przykładowe dane features (demonstracja)
np.random.seed(42)
n_samples = 1000
X = pd.DataFrame({
'powierzchnia': np.random.normal(70, 25, n_samples),
'liczba_pokoi': np.random.randint(1, 5, n_samples),
'wiek_budynku': np.random.randint(0, 50, n_samples),
'odleglosc_centrum': np.random.exponential(5, n_samples)
})
# Oblicz korelacje między features
correlation_matrix = X.corr()
# Przygotuj wykres
plt.figure(figsize=(8, 6))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', center=0)
plt.title('Korelacje między features')
plt.close()
print("Macierz korelacji między zmiennymi:")
print(correlation_matrix)
print("\nInterpretacja:")
print("• Wartości blisko 1.0 = silna korelacja pozytywna")
print("• Wartości blisko -1.0 = silna korelacja negatywna")
print("• Wartości blisko 0.0 = brak korelacji")
print("\nJeśli korelacja między features > 0.8, usuń jedną z nich (multicollinearity)!")
plt.figure(figsize=(8, 6))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', center=0)
plt.title('Korelacje między features')
plt.show()
Pokaż mapę korelacji
Macierz korelacji między zmiennymi:
powierzchnia liczba_pokoi wiek_budynku odleglosc_centrum
powierzchnia 1.000000 -0.064763 0.033920 0.029856
liczba_pokoi -0.064763 1.000000 -0.003894 -0.057555
wiek_budynku 0.033920 -0.003894 1.000000 -0.037242
odleglosc_centrum 0.029856 -0.057555 -0.037242 1.000000
Interpretacja:
• Wartości blisko 1.0 = silna korelacja pozytywna
• Wartości blisko -1.0 = silna korelacja negatywna
• Wartości blisko 0.0 = brak korelacji
Jeśli korelacja między features > 0.8, usuń jedną z nich (multicollinearity)!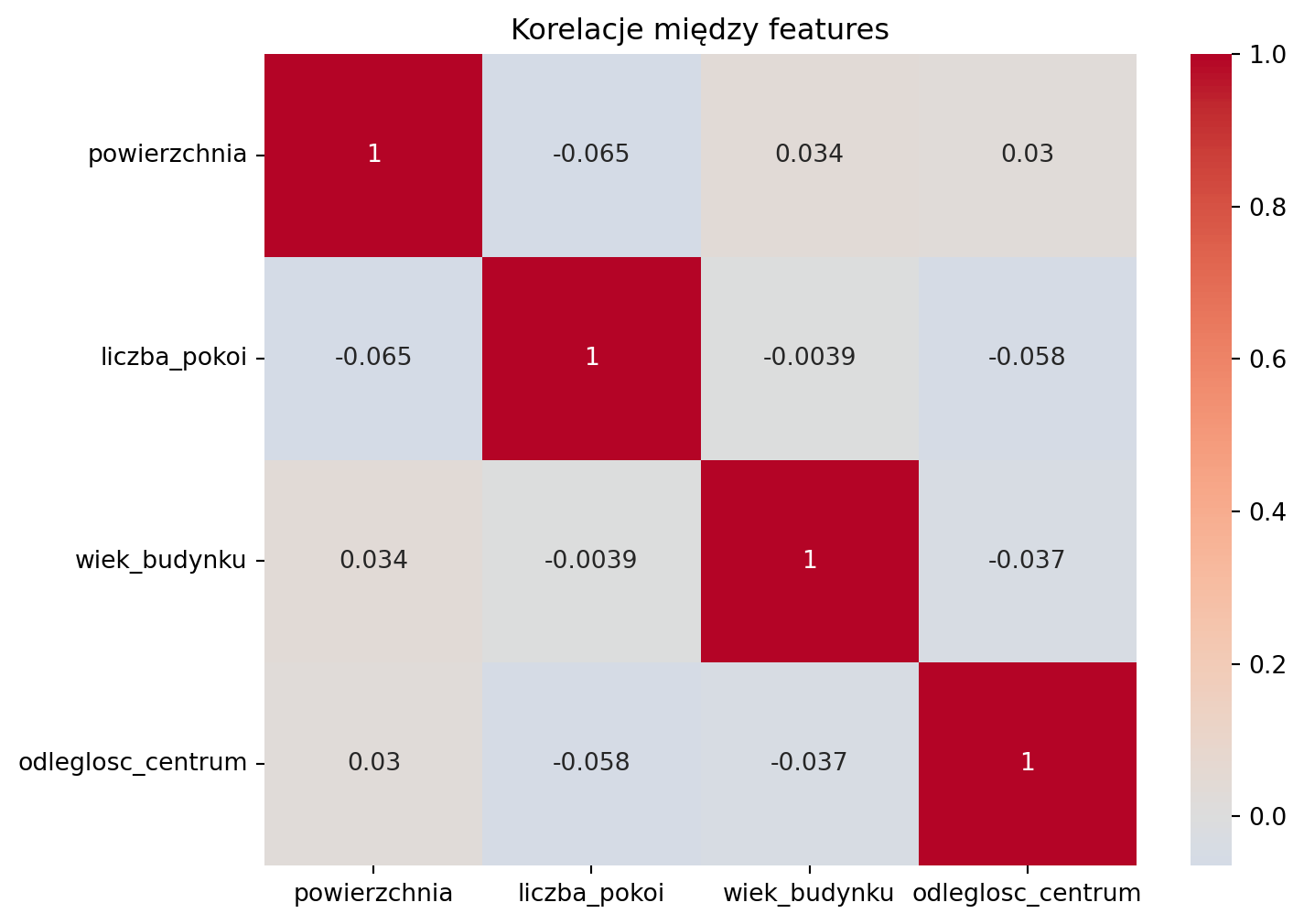
Jeśli korelacja między features > 0.8, usuń jedną z nich!
🔧 Parametry do tuningu
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.pipeline import Pipeline
# 1) Standardization - gdy features mają różne skale
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_train)
# 2) Polynomial Features - dla nieliniowych zależności
poly_model = Pipeline([
('poly', PolynomialFeatures(degree=2)),
('linear', LinearRegression())
])
poly_model.fit(X_train, y_train)
poly_pred = poly_model.predict(X_test)
poly_r2 = r2_score(y_test, poly_pred)
print(f"Polynomial Regression R²: {poly_r2:.3f}")
# 3) Regularization - Ridge i Lasso
from sklearn.linear_model import Ridge, Lasso
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, y_train)
ridge_r2 = r2_score(y_test, ridge.predict(X_test))
lasso = Lasso(alpha=1.0)
lasso.fit(X_train, y_train)
lasso_r2 = r2_score(y_test, lasso.predict(X_test))
print(f"Ridge R²: {ridge_r2:.3f}")
print(f"Lasso R²: {lasso_r2:.3f}")
Pokaż wyniki predykcji cen
Polynomial Regression R²: 0.933
Ridge R²: 0.934
Lasso R²: 0.934🌍 Real-world przykłady zastosowań
- E-commerce: Przewidywanie wartości życiowej klienta (LTV)
- Nieruchomości: Automatyczna wycena domów (Zillow)
- Finanse: Scoring kredytowy, przewidywanie cen akcji
- Marketing: ROI kampanii reklamowych
- Supply Chain: Prognozowanie popytu na produkty
💡 Kiedy używać Linear Regression?
✅ UŻYJ GDY:
- Przewidujesz wartości liczbowe (continuous target)
- Zależności wydają się liniowe
- Chcesz interpretowalny model
- Masz stosunkowo mało features
❌ NIE UŻYWAJ GDY:
- Target jest kategoryczny (użyj klasyfikacji)
- Zależności są bardzo nieliniowe (użyj Random Forest, XGBoost)
- Masz tysiące features (użyj regularization)
Następna ściągawka: Decision Trees - klasyfikacja 🌳